中国混凝土病害诊治研究院：大气环境下钢筋混凝土桥梁剩余寿命预测与耐久性评估
闻宝联1 田冠飞2
（1.国家建筑材料工业技术监督研究中心，北京，100024；2.中国建筑科学研究总院，北京，100860）
摘 要：分析了大气环境下钢筋混凝土桥梁的损伤机理和失效模式，引入了混凝土碳化和钢筋锈蚀的预测模型，建立了混凝土构件耐久性极限方程，对桥梁构件进行了可靠性分析，并基于由碳化和钢筋锈蚀引起的裂缝控制标准进行了剩余寿命预测，最后引入模糊数学概念，利用三级模糊综合评判评定了桥梁结构的耐久性等级。
关键词：钢筋混凝土；桥梁；剩余寿命；耐久性
引言
钢筋混凝土桥梁在使用过程中，要受到环境、有害化学物质的侵蚀，并承受车辆、风、地震、疲劳、超载、人为因素等外来作用，加之自身性能的不断退化，导致桥梁结构各部分不同程度的损伤和劣化。而旧桥是巨大的资源，通过旧桥可靠性评估，进行既有桥梁剩余寿命的预测，挖掘旧桥潜力，无疑可以节约能源、资源，保护环境，具有明显的经济效益和社会效益。
1 混凝土碳化的数学模型
混凝土的碳化会导致钢筋锈蚀，其结果是结构在预定时间内、规定条件下完成预定功能的能力下降[1]。
混凝土的碳化区由完全碳化区和部分碳化区组成，部分碳化区的存在是二氧化碳在混凝土中的扩散速度大于其与混凝土中可碳化物质反应速度而造成的。研究表明，钢筋在部分碳化区同样可能发生锈蚀。
1.1 完全碳化深度[2]
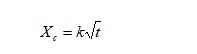
－碳化深度，mm;
－完全碳化系数，mm/a0.5;
－服役时间，a;
1.2 部分碳化区深度[3]
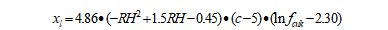
xl－部分碳化区深度（mm）
RH－环境相对湿度，%
－混凝土抗压强度（MPa）
2 钢筋锈蚀数学模型
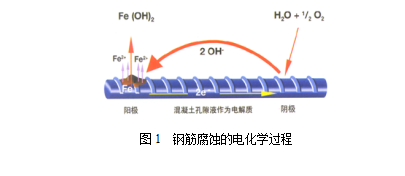
大气环境下，钢筋混凝土的损伤过程为：混凝土碳化、钢筋脱钝、锈蚀，承载力不足引起结构失效。根据其损伤机理，分为以下过程[4]（如图1）
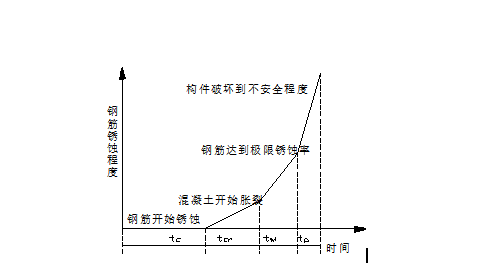
图1 混凝土中钢筋腐蚀示意图
根据金伟良的研究结果[5]，钢筋在不同阶段的锈蚀率可以表示为
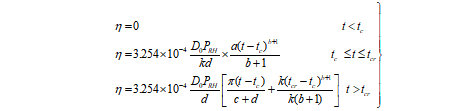（3）
D0—氧气在混凝土中的扩散系数（mm2/a）
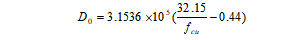（4）
d—钢筋直径，mm
c—保护层厚度,mm
a,b—与混凝土性能有关的系数，可从文献[5] 中查表得到。
—考虑仅当大气相对湿度大于钢筋锈蚀的临界相对湿度时,钢筋才发生锈蚀而对钢筋锈蚀量进行的修正，取为60%
根据文献[5]，引起钢筋混凝土胀裂的钢筋锈蚀率可表示为
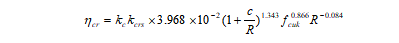（5）
为混凝土胀裂锈蚀率
为钢筋半径,mm
钢筋种类修正系数，对变形钢筋取1.23，光圆钢筋1.0
为钢筋位置修正系数，对边中位置取1.33
3 钢筋混凝土桥梁剩余寿命预测
构件的剩余寿命预测是结构评估的基础，进行寿命预测，必须先定义失效准则，也就是极限状态。
钢筋混凝土构件的耐久性极限标准因对象的不同，所处的环境不同和重要性的不同而易。对大气环境下的混凝土构件，可以认为碳化是钢筋锈蚀的主要原因，钢筋锈蚀会导致混凝土表面发生裂缝，根据裂缝控制等级，划分构件的耐久性极限标准[6]
表1 构件纵向裂缝宽度的耐久性极限指标
构件裂缝控制等级 | 纵向裂缝控制宽度 |
一级 | 钢筋开始脱钝锈蚀 |
二级 | 混凝土保护层胀裂 |
三级 | 纵向裂缝宽度w<=0.3mm |
为说明问题，先进行一算例分析
某桥梁主梁混凝土设计标号为C25，采用325普硅水泥，水灰比0.6，粉煤灰等量取代10%，自然养护。投入使用时间15年，经回弹检测，混凝土强度符合N（35.64，4.532）正态分布，完全碳化深度符合N（12.68，3.652）正态分布，保护层厚度符合N（35.26，4.462），光圆钢筋直径20mm，计算剩余寿命。根据其在桥梁中的作用，假设其为裂缝控制等级二级。1）计算部分碳化深度根据前式，计算得到混凝土部分碳化深度为14.56mm2）根据混凝土完全碳化区长度，可得完全碳化系数满足N（3.25，0.942）。
3）当部分碳化深度达到钢筋时，假设钢筋锈蚀开始，计算得到tc=40.6年；=6.2%；tcr=45.8年，则预测寿命为40.6+45.8=86.4年，剩余寿命86.4-15=71.4年
4 桥梁耐久性评估
本文中，套用《钢铁工业建（构）筑物可靠性鉴定规程》（YBJ219-89）的评价方法，利用耐久性系数进行评定，为构件预测剩余寿命，为设计剩余寿命
表2 单一构件耐久性等级评定标准
等级 | a | b | c | d |
|
| [1.0,1.5) | [0.75,1.0] | <0.75 |
而按此标准评定，有很多不尽合理之处，如Kn=1.001与1.499处于一个级别，相差0.498，与Kn=0.999相差0.002，却分属两个级别。为克服这一缺陷，引入模糊数学中隶属函数来进行处理。
a级隶属函数为
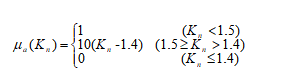（6）
b级隶属函数为
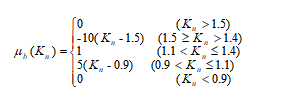（7）
c级隶属函数
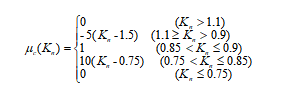（8）
d级隶属函数
（9）
对于桥梁而言，可以将桥梁按其结构体系组成分三级进行评估。(1).进行基本单元（如基础、桥墩、主梁、桥板等）评价，然后构造样本评判矩阵，引入传力树概念建立构件权重集，最后求得构件评判结果。(2).由（1）的评判结果构造分项工程评判矩阵，用分项工程的权重集求得分项工程评判结果，(3).由（2）的评判结果构造整体桥梁的评判矩阵，最后用整体桥梁结构的权重集给出耐久性评价。
下面结合具体算例进行桥梁的耐久性评价。
有一座三跨混凝土简支桥，跨距相等，各构件经过剩余寿命预测和等级划分，得到对应等级的隶属函数，按前述方法进行耐久性评价。
1）构造一级耐久性评判
附属设施R25=[0 0.86 0.14 0]
各构件的权重可以按个构件承担的平面荷载面积相对大小进行取值，由此，得到每个构件的权重集。
地基A11=[1/6 1/3 1/3 1/6]
基础A12=[1/6 1/3 1/3 1/6]
桥墩A21=[1/6 1/3 1/3 1/6]
主梁A22=[1/6 1/6 1/6 1/6 1/6 1/6]
次梁A23=[1/12 1/12 1/12 1/12 1/12 1/12 1/12 1/12 1/12 1/12 1/12 1/12]
桥面板 A24=[1/3 1/3 1/3]
在获得不同类别构件的评判矩阵和相应的权重集后，由Bij=Aij·Rij就可计算其耐久性评判结论。
地基B11=[0.3254 0.6746 0 0]
基础B12=[0.6610 0.3390 0 0]
桥墩B21=[0.8784 0.1216 0 0]
主梁B22=[0.1530 0.4915 0.3555 0 ]
次梁B23=[0.1717 0.6083 0.2200 0]
桥面板 B24=[0 0.7590 0.2310 0]
附属设施B25=[0 0.86 0.14 0]
2)构造二级（分项工程）耐久性评判
附属设施
R3= [0 0.86 0.14 0]
由于地基和基础承受的平面载荷相等，故权重集为A1=[0.5 0.5]
桥墩、主梁、次梁、桥面板承重一样，故其权重集为A2=[0.25 0.25 0.25 0.25]。
由Bi=Ai·Ri到分项工程的耐久性评判结论
下部承重结构：
B1=[0.4932 0.5068 0 0]
上部承重结构
B2=[0.3008 0.4951 0.2016 0]
附属设施
B3=[0 0.86 0.14 0]
3）构造三级（桥梁整体）耐久性评估
由上一步，得到桥梁整体结构的评判矩阵
对于桥梁，上部结构与下部一样重要，而附属设施的重要性要差一些，则其权重集为
A=[0.45 0.45 0.1]
由B=A·R得到整体评判结论
B=[0.3573 0.5369 0.1047 0]
4）用贴近度法划分结构耐久性等级
本文引入贴近度法进行评判，假设为评判等级集，等级中最理想的子集是（0 0 1 0 0 0…..），记为Di，其中1是第i个分量，对任何评判向量B，都可以计算其与理想目标的贴近度，这样可以有效利用所有信息，贴近度法分为对称贴近和非对称贴近法，对称贴近是将元素置于相同地位，非对称贴近是将元素置于不同地位，本文中评价矩阵元素地位不同，用非贴近法，如（10）式。
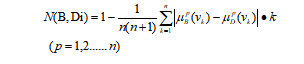（10）
式中：
—B所对应对象隶属于的隶属度；
—用于等级划分时取1即可
N（B，Di）为用以评价结论B与标准评判结论Di的接近程度。为计算方便
首先将B标准化，即µBi=[bi bi-1 bi+1 bi-2 bi+2……],这样可以直接与µD1[1 0 0 0]进行比较
µB1=[0.3573 0.5369 0.1047 0]
µB2=[0.5369 0.3573 0.1047 0]
µB3=[0.1047 0.5369 0 0.3573]
µB4=[0 0.1047 0.5369 0.3573]
计算得到：
=(0.898,0.925,0.830, 0.788)
由此可见，评判结果最大，评定为b级。
5结论
钢筋混凝土结构中混凝土碳化、钢筋锈蚀是客观存在的，并遵循着一定的规律影响着结构性能，基于碳化和钢筋锈蚀模型对桥梁的寿命进行预测和可靠性评估是可以接受的，结合桥梁运营概况和设计参数，利用该方法进行检测、评估是比较简单易行的方法。
参考文献
[1]贡金鑫，赵国藩，赵尚传. 大气环境下锈蚀对钢筋混凝土结构可靠度的影响. 大连理工大学学报[J],2000（2）:210-213
[2]张誉，蒋利学，张伟平等. 混凝土结构耐久性概论[M].上海科学技术出版社.2003.12
[3]牛荻涛. 混凝土结构耐久性与寿命预测[M]. 科学出版社.2003.2
[4]洪定海. 混凝土中钢筋的腐蚀与保护[M].中国铁道出版社.1998
[5]金伟良. 赵羽习.混凝土结构耐久性[M].科学出版社.2002.9
[6]黄有志. 既有混凝土桥梁可靠性分析[D].浙江大学硕士论文.2001.2
